初心者のためのDjango入門
■第22話:SciPyを用いた最適化計算
(最終更新日:2023.07.12)

(絵が小さい場合はスマホを横に)
「SciPyを用いて最適化計算をしてみよう!」
SciPy(サイパイ)は、Pythonで科学計算を行うためのオープンソースのソフトウェアライブラリで、
統計の難しい計算や最小化した値を見つける計算を瞬時に行うことができる。
今回は、そんな計算方法の一部を紹介する。
[目次]
1.SciPyによる統計計算
scipy.statsモジュールは、統計的分析と確率過程を行うためのツールを提供する。 これには、約80以上の連続確率分布(正規分布、一様分布、ガンマ分布など)と10以上の離散確率分布(ポアソン分布、二項分布など)、 そしてそれらの分布の統計関数が含まれます。今回は正規分布の確率密度関数のグラフを表示する例を示す。 コードは以下の通りである。scipy.statsで、-3~3までの正規分布の確率密度関数を作成し、matplotlibでグラフ化している。 作成したグラフはコードの下に示す。

-3~3までの正規分布の確率密度関数
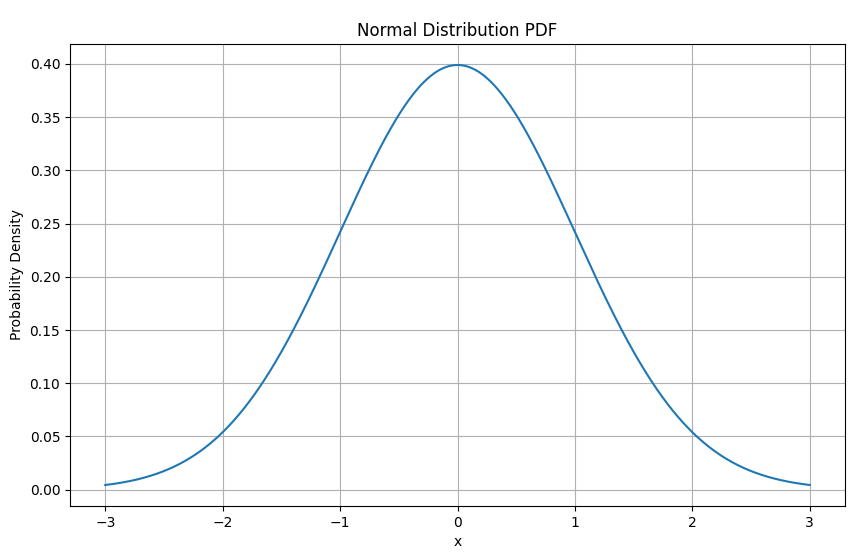
正規分布の確率密度関数のグラフ
このようにPythonのscipy.statsモジュールを用いることで、統計的な関数や計算、グラフ化を短いコードで簡単に求めることができる。
2.SciPyによる最適化計算
scipy.optimizeモジュールは、関数の最小化(または最大化)、根の求め方(例えば、非線形方程式の解を見つける)、 曲線のフィッティングなど、最適化問題を解くための機能を提供します。 下記のコードの例では「y = x^2 + 10sin(x)」の式のyの最小値を求められる。 実際計算させると、xが-1.306の時に最小値-7.946を取ると出る。

関数の最小化
先ほどの式をmatplotlibでグラフ化すると、計算した値が合っていることが分かる。 xが-1.306付近で最小値-7.946になっている。 このように、非線形的な難しい最小値の計算もScipyを使えば瞬時に算出できる。
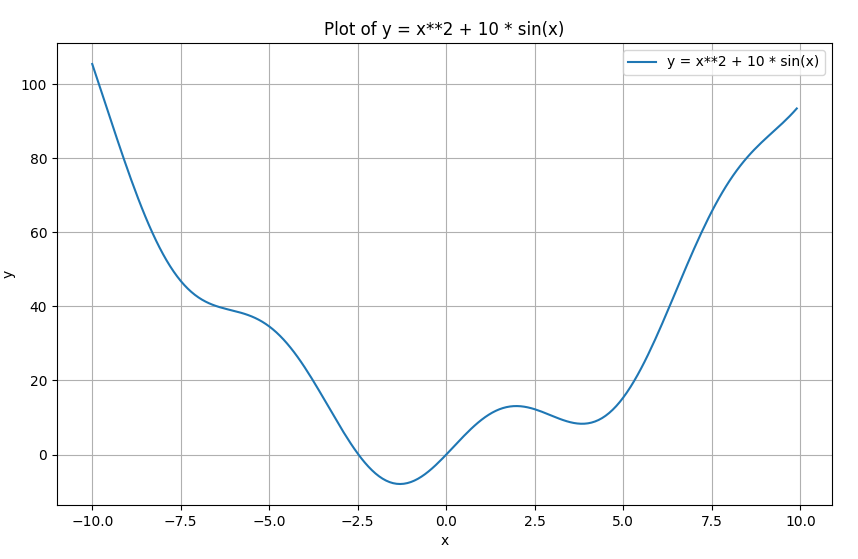
上記の関数のグラフ
次に「y = x^2 -9」の解を求めてみよう。これくらいの二次方程式であれば、 因数分解して3と-3であることは簡単に解けるが、 もう少し複雑な高次の方程式はコンピューターを使わないと厳しい。 合っているかの確認をしたいので、Scipyを使って計算すると、0から走査して(下記のx0=0で設定)調べると3が導びかれ、 -5から走査すると-3が導びかれる。

高次の方程式の解の導出
3.まとめ
今回はSciPyによる統計計算と最適化計算について紹介した。 最適化計算は、通常算出するのが難しいような値もScipyを使えば瞬時に計算できる。 ぜひ、機会があるときに使ってみよう。
▼参考図書、サイト
1. Pythonで学ぶ統計学 2. 確率分布[scipy.stats徹底理解] Qiita
SciPy.optimize:解の求め方と最適化問題 経済学のためのPython入門